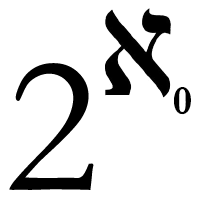Mathy Stuff

Workshop #6

We will start with some insight warm ups. You may not spend more than 15 minutes each on numbers 1 and 2.

1. Explain why the only conceivable computer number system is base 10.

2. Solve for x, where the ellipses means the exponentiation is repeated forever (aka infinite tetration). (e is the exponential constant with e≈2.71828183...)

   ⋰

   _x

   e = x^x

3. Let S be a set of real numbers which is closed under multiplication (that is, if a and b are in S then so is ab). Let T and U be disjoint subsets of S whose union is S. Given that the product of any three (not necessarily distinct) elements of T is in T and that the product of any three elements of U is in U, show that at least one of the two subsets T, U is closed under multiplication.

4. 4) Of two unknown integers between 2 and 99 (bounds included) a person P is told the product and a person S is told the sum. When asked whether they know the two numbers, the following dialog takes place:

   P: I don't know them.
   S: I knew that already.
   P: Then I know now the two numbers.
   S: Then I now know them too.

   With the above data determine the two numbers, and establish that your solution is unique.