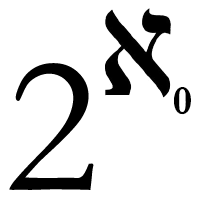Workshops
Workshop #1
-
In your reading from Thinking Mathematically the first example problem asks you to find out whether you would pay less if the tax is calculated before or after the discount. Does either scenario sound unrealistic? In either case, is there a more realistic calculation that you could do than the one given in the book where the discount is calculated first? Or what about when the tax is calculated first?
-
-
Prove this De Morgan’s law: ¬(A ∨ B) ≡ ¬A ∧ ¬B
-
Now see if you can come up with two or three distinct ways to prove De Morgan’s other law: ¬(A ∧ B) ≡ ¬A ∨ ¬B
-
-
Subtraction Games are two-player games where you have a pile of beads and a previously chosen set S of positive whole numbers (for example, S = {1,3,4}); you take turns choosing one number from the set S and taking that many beads from the pile, no more and no less. If there is no viable move or no more beads you lose.
-
So clearly the first player wins with the example set above and any pile of size 1, 3, or 4 but loses for a pile of size 0 or 2. When can the first player win (that is, for which pile sizes n can the first player win)? Using induction, prove that you are right for this set S = {1,3,4} and a pile of size n. What is the strategy? Using induction, prove that your strategy works.
-
Now do the same for the set S = {2,5,6}.
-
Look for a general way of finding a strategy to win, with a given finite set S. i.e. give an algorithm that describes this procedure.
-