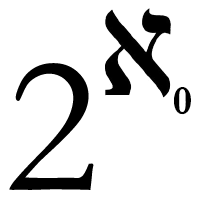Workshops
Workshop #2
If you do not know where to start, look on the inside of the back cover of Cupillari. Some problems are taken from Cupillari or USSR Olympiad problem book, possibly with slight modifications.
Discuss the truth value of the statements in problems 1-4. Prove or disprove them accordingly.
-
There is a unique prime equal to n5 - 1 for some positive integer n.
-
The difference of two irrational numbers is always an irrational.
-
Let A, B, C, D be subsets of U. (Where if Δ ⊆ U, Δc = {x ∈ U | x ∉ Δ})
-
(A - B) ∩ C = A ∩ (Bc ∩ C)
-
(A ∪ B ∪ C)c = Ac ∪ Bc ∪ Cc
-
(A ∪ B) ∪ (C ∩ D) = (A ∪ B ∪ C) ∩ D
-
-
-
n3 - n is divisible by 3
-
n5 - n is divisible by 5
-
n7 - n is divisible by 7
-
If c is odd then nc - n is divisible by c.
-
Venn Diagrams are useful for conjecture but will not qualify for proof and disproof for the next statements.