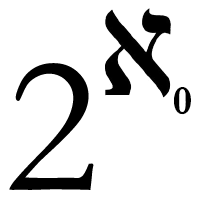Mathy Stuff

Workshop #3

Some problems are taken from the USSR Olympiad problem book, possibly with slight modifications.

1. Take any set A with n elements, now look at the set B = {0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011,..., 11[n 1s in a row]11} which is the set of numbers 0, 1, 2, 3, 4, ... written in binary. Relate the subsets of A to the elements of B.

2. Take a look at the following triangle where each number is the sum of the number above it and the two numbers to the left and right of that number. If no number is located in any of these specified positions, 0 is used in that position.

   
   1
   111
   12321
   1367631
   ⋰⋮⋮⋮⋮⋮⋱

   Prove that every row after the second contains a non-zero even number.

3. Subtraction Games again: Find who wins and a winning strategy for a game with pile size n for the following subtraction sets, and answer the question that follows. (IMPORTANT: remember the strategies you find for problem 4.)(If you do not remember the rules of the game, or weren’t here week one, ask me.)

   1. {2,4,7} At what pile size does the win loss pattern become periodic?

   2. {2,5,7} What is the period of the win loss pattern for this game?

4. Now what if you take multiple games, and play them simultaneously, in other words you have two piles and each move consists of moving in only one pile, then the other player moves. The objective is still the same, leave the other player without a valid move. For example if you can take an element of {2,4,7} from any single pile on your turn, and the board has one pile of size 4, and the other pile of size 2, you would want to take 2 beads from the pile with size 4, and that is the only winning move.

   1. Find an optimum strategy given two piles and the subtraction set is {1,2,3}

   2. What about 3 or n piles?

   3. Now do what you did in parts a. and b. for the subtraction set {1,2,4}.

   4. Now do the same for the subtraction set {2,5,7}.

   5. What about 2 piles but the subtraction set is the positive integers? What about n piles?

   6. If you are done come and ask me about the rules to the game of Kayles and the class of Octal games.